GRAPH

Graph adalah kumpulan dari vertex dan edges. Dalam data structure, vertex bisa dibilang sebagai suatu node, sedangkan edges adalah garis penghubungnya. Graph ada 2 jenis, yaitu directed dan undirected. Directed adalah edges yang memiliki suatu arah ke suatu vertex tertentu sedangkan undirected tidak.

MST (Minimum Spanning Tree)
Untuk dapat mencari MST terdapat 3 cara, yaitu:
1. Prim’s Algorithm
Ketika akan membuat MST, tidak boleh ada edge yg dapat menyebabkan looping. Cari jalan yg costnya terkecil dari setiap path.
2. Kruskal’s Algorithm
Verteks yg sudah dikunjungin ditulis, lalu dilanjutkan terus sampai adjacency list habis, kemudian dicek apakah terjadi looping atau tidak. Jika sudah selesai, dicek apakah semua vertex sudah dikunjungi.
3. Dijkstra’s Algorithm
Dijkstra Algorithm biasanya digunakan untuk menentukan minimum path dari verteks ke verteks lain. Berbeda dengan Prim’s dan Kruskal’s Algorithm yang mencari minimum path dari semua verteks yg terdapat di graph.

Heap

Completed binary tree yang diimplementasikan menggunakan array, setiap elemen disimpan secara berurutan, root disimpan di index 1.

Ada 3 macam Heap:

• Min-Heap : Root paling kecil. Child node nya selalu lebih besar dari parent nodenya
• Max-Heap : Root paling besar. Child node nya selalu lebih kecil dari parent nodenya
• Min Max-Heap : Nilai min dan max bergantian terus-menerus, dimulai dari min.

Operasi pada Min-Heap:

• Find: langsung ambil node paling atas karena datanya sudah urut.
• Insert: masukan node baru ke tempat paling bawah kemudian bandingkan dengan parentnya sampai nilai parentnya lebih kecil dari pada node tersebut, sampai node tersebut berada ditempat yang benar.
• Delete: node yang dihapus akan di gantikan dengan node paling bawah, dan node tersebut akan dibandingkan dengan node dibawahnya sampai menempati tempat yang benar.

Operasi Max-Heap:

Operasinya sama dengan min-heap, tapi sesuai dengan syarat max-heap.

Operasi Min max-Heap

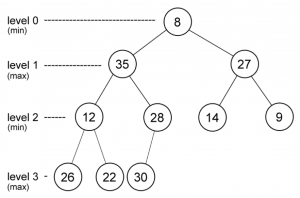
• Nilai min pada level genap, nilai max level ganjil
• Insert : Masukan node pada paling bawah, bandingkan dengan parentnya sesuai dengan ketentuan level, jika nilai tersebut aadalah nilai paling min maka upheapmin dengan node root, atau lakukan upheapmax pada node level ganjil  pertama dengan  node paling max.
• Delete : dapat dilakukan dengan delete min dan delete max. Jika delete min, maka root langsung dihapus dan delete max, maka angka max dari children root akan dihapus dan node tersebut diganti dengan node paling bawah. Lakukan downheapmax pada nilai max, dan downheapmin pada node nilai min.

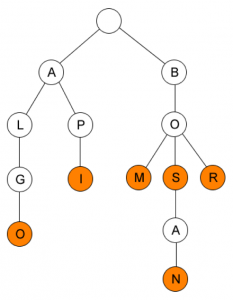
Tries

ordered tree struktur data yang digunakan untuk menyimpan asosiatif array, biasanya string. Rootnya berisi karakter kosong.

Hashing

 transformasi sebuah string dari karakter menjadi nilai yang merepresentasikan string aslinya. berfungsi untuk mempercepat proses pencarian karena dinilai lebih cepat ketimbang mencari dengan karakternya.

 

RED-BLACK TREE

• Insert

New node = red.

1. parent and uncle of new node is red, change parent and uncle color to black and grandparent color to red.
2. parent of the new node is red and uncle is black, do rotation (LL, RR, LR or RL).

• Delete

1. the node being deleted has a red-colored parent and a black-colored child, then the child can be replaced directly.
2. the node being deleted has a black-colored parent and a red-colored child, the child could replace the node but it has to change color from red to black.

2-3 TREE

2 jenis node:

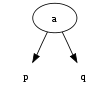
• node 2 : tidak punya anak atau punya 2 anak.  contoh node a, p dan q boleh null boleh memiliki value :

• node 3: tidak punya anak atau punya 3 anak. contoh node ab, p, q dan r boleh null boleh memiliki value : 

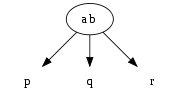
2-3 Tree harus simetris, artinya perbedaan level kiri dan kanan harus sama.

• Insert

1. Selalu insert mengisi yang kosong dari paling atas. kalau dari bawah kosong, cek dulu parentnya, apakah kosong atau tidak, jika kosong, naik lagi sampai terisi bagian atas semua. (dengan kata lain semakin terisi semakin ke atas)

• Delete

1. Jika yang di delete adalah leaf node, langsung delete saja.
2. Jika bukan, harus dilakukan reposisi. (lakukan yang paling memungkinkan dan tidak menyalahi aturan)

---

---

BALANCED BINARY TREE

Salah satu Balanced Binary Tree adalah AVL. AVL itu sendiri adalah jenis binary tree yang memiliki balance factor atau perbedaan level / tinggi nya tidak boleh melebihi 1 antara substree kiri dan kanannya. Manfaat atau tujuan dari AVL tree itu sendiri adalah menyeimbangkan binary search tree agar lebih mudah proses pencarian / searching nya.

Konsep AVL Tree :

1. Height dari sub tree yang kosong adalah 0.
2. Height dari leaf adalah 1.
3. Height dari internal node adalah max height dari anaknya + 1.

Balance Factor :

1. Perbedaan height dari subtree kiri dan kanan.
2. Selisih ketinggian hanya boleh bernilai 1 / 0.

Menyeimbangkan AVL membutuhkan salah satu atau 2 dari 2 proses rotation.

Single Rotation

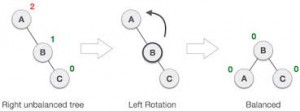
Double Rotation 

Ada 2 proses dalam AVL yaitu insertion dan deletion.

INSERTION

Insert biasa seperti binary tree namun selalu cek balance factornya setiap kali insert, jika tidak memenuhi ketentuan AVL, maka lakukan penyeimbangan dengan single atau double rotation tergantung kondisi.

DELETION

Delete biasa seperti binary tree dengan 3 kondisi, delete leaf, delete parent 1 anak, delete parent 2 anak, lalu cek balance factornya, jika tidak memenuhi ketentuan AVL, maka lakukan penyeimbangan dengan single atau double rotation tergantung kondisi.

---

---

 

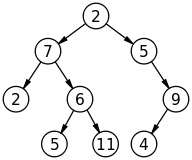
BST
merupakan singkatan dari binary search tree. BST merupakan sebuah binary tree yang subtree kiri nya lebih kecil valuenya dibandingkan dengan root nya. sedangkan subtree kanan nya lebih besar atau sama valuenya dibandingkan dengan root.

Operasi dalam BST

Deleting
Delete sendiri ada 3 kondisi. pertama, jika kita ingin menghapus sebuah leaf atau node yang tidak memiliki child, kita tinggal menghapusnya saja. kedua, jika node yang ingin dihapus memiliki 1 child, kita tinggal menghubungkan child si node tersebut dengan parent nya node tersebut, lalu delete node tersebut. ketiga kalo node yang ingin dihapus memiliki 2 anak, bandingkan lalu pilih node dengan value yang lebih besar untuk menggantikan node tersebut.

Searching
Proses ini fungsinya mencari apakan node/value yang kita cari ada didalam tree atau tidak. cari dari root, jika bukan root, bandingkan dengan root jika lebih kecil cari ke subtree kiri, jika lebih besar cari ke subtree kanan, begitu seterusnya sampai value ketemu. jika tidak, maka value/node tersebut tidak ada didalam tree.

Inserting
Proses ini berguna untuk menambah sebuah node atau value kedalam tree. pertama, cek jika tidak ada root atau dengan kata lain tree masih kosong, maka insert data akan menjadi root, jika sudah ada.. maka cek jika lebih kecil dari root maka insert ke kiri, jika lebih besar insert ke kanan. terus bandingkan sampai mendapat posisi yang tepat.

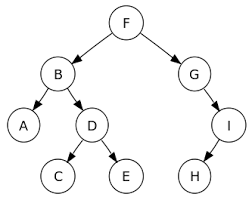
Root : node yang berada di paling atas.

Edge : garis yang menghubungi parent dan child.

contoh: garis yang menghubungkan A dan B.

Height/Depth : maksimal degree dari node di dalam tree.

Height : 4.

Parent D adalah B.

Children D tidak ada, sedangkan children C adalah E dan F.

Leaf : node yang tidak memiliki children

contoh: D

Sibling : node yang memiliki orang tua yang sama

contoh : H dan I

Degree sebuah node : jumlah sub tree sebuah node

A dihubungkan ke B, maka A adalah ancestor dari B dan B adalah descendant dari A.

Binary Tree

tree yang setiap cabangnya memiliki maksimal 2 cabang.

cabang yang kanan disebut right child dan yang kiri disebut left child.

Perfect binary tree : binary tree yang setiap levelnya memiliki depth yang sama.

Complete binary tree : binary tree yang setiap levelnya, kecuali mungkinan yang terakhir terpenuhi dan semua node nya berada di kiri.

Skewed binary tree : binary tree yang masing-masing nodenya memiliki hanya 1 cabang.

Balanced binary tree : binary tree yang jarak root ke leaf nya sama dengan jarak antara cabang yang kanan dan yang kiri.

 

PERTEMUAN KE 3.

Queue

Dalam Queue kita bisa menambahkan sebuah data ke ujung bagian belakang dan untuk menghapus kita dapat menghapus bagian terdepan. jadi prinsip nya adalah data yang pertama kali masuk adalah juga yang pertama kali keluar, itulah mengapa Queue disebut juga sebagai First in First Out (FIFO). Penambahan data baru dilakukan di rear (belakang) dan penghapusan dilakukan di front (depan).

Jika Front = Rear = NULL, maka queue kosong.

Beberapa aplikasi penggunaan queue: Priority Queues dan Breadth First Search.

 

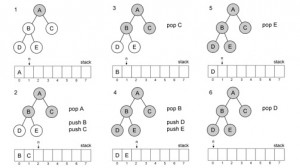
Stack

Kita dapat menambahkan data ke dalam stack, stack sendiri sering digambarkan sebagai menara vertikal, kita dapat menambahkan data baru ke bagian atas terus menerus hingga bertumpuk namun yang pertama kali keluar adalah bagian teratas atau data terakhir yang kita tambahkan, Itulah mengapa stack disebut Last In First Out (LIFO).

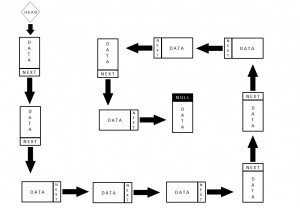
Dalam linked stack, minimal setiap node mempunyai 2 bagian:

• satu untuk menyimpan data
• satu untuk menyimpan alamat ke node selanjutnya,
• namun, dapat ditambah satu untuk menyimpan alamat node sebelumnya (double linked list)

Depth First Search (DFS)

Algoritma untuk melintas/mencari dalam tree/graph.

Breadth First Search (BFS)

Seperti DFS, sebuah algoritma untuk melintas/mencari dalam tree/graph.

DFS menggunakan stack, namun BFS menggunakan queue.

Infix, Prefix, Postfix

Prefix : Operator Operand Operand
Postfix : Operand Operand Operator
Infix : Operand Operator Operand

 

Pada pertemuan kedua data structure kami kedatangan seorang dosen tamu bernama Bong defendy, beliau adalah seorang lulusan Bina Nusantara Tahun 2007 dan beliau saat ini bekerja di Datacaraka Solusindo, PT Easytech Indonesia.

beliau menjelaskan kepada kami beberapa hal yang nantinya akan kami hadapi dalam dunia IT, yaitu;

BIG DATA

seiring dengan banyaknya data yang perlu di proses.. karena pengguna internet pun semakin meningkat dengan pesat akhirnya muncullah istilah big data karena banyak nya data yang perlu di gunakan dan diakses dalam waktu yang bersamaan.

ARDUINO

yang saya tangkap arduino sendiri mirip dengan sebuah perangkat komputer, bisa menerima input kemudian melakukan proses sehingga dapat memberikan output namun memiliki ukuran yang sangat kecil bila dibandingkan dengan perangkat komputer. bertujuan untuk mempermudah berbagai kegiatan manusia.

SMART HOUSE TECHNOLOGY

Teknologi terbaru yang berujuan untuk mempermudah penghuni rumah dalam menjaga, monitoring, sensor, dan mengkoneksi rumah dengan penghuni lebih efektif.

Contoh yang nyata yang saya temukan adalah seperti handphone atau tablet yang sudah dapat mematikan dan menyalakan berbagai perangkat seperti printer, TV, AC, dan lainnya.

 

ada dua memory allocation, pertama static memory allocation dan yang kedua adalah dynamic memory allocation.

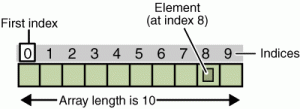
contoh dari static memory allocation adalah array.

Array sendiri bersifat homogen, yang berarti tipe data yang didalamnya sama dan dapat dipanggil berdasarkan index, mengapa? Karena dalam kenyataannya, static memory allocation akan menyediakan tempat yang bersebelahan.

kemudian dynamic memory allocation contohnya adalah Linked List.

kemudian ada 3 cara memasukkan sebuah nilai kedalam array.

• Initialize = array[3] = {6,8,2}
• assigning = dari program itu sendiri. contohnya >> array[5] = array[6]
• Inputing = input dari user lalu di scan oleh program.

pointer (*)

misal kita menggunakan pointer b berdasarkan data a. maka data b akan sesuai atau sama dengan data a, misal kita ganti data a, maka data b pun juga akan berganti.

ada juga double pointer (**) yang akan point ke single pointer, dan seterusnya.

Queue (FIFO)

FIFO diatas berarti First in First out, jadi yang pertama masuk akan menjadi yang pertama keluar, persis dengan logika jika kita sedang dalam antrian. namun ada juga priority, dimanapun posisi nya akan diutamakan, sebagai contoh sedang antri tiket bus namun ada ibu hamil maka ibu hamil (priority) akan didahulukan.

ada juga circular, bentuk antriannya memutar.

Stack (LIFO)

LIFO diatas berarti last in first out. seperti sesuatu yang menumpuk, jika kita taruh benda terakhir (last in) di paling atas, maka jika akan kita ambil benda teratas tersebut akan pertama kali diambil (first out).

Binary Trees.

Binary trees memiliki 2 cabang kaki.

Binary Search Trees.

Memiliki 2 cabang, dan cabang kiri lebih kecil dari bagian atasnya sedangkan cabang kanan lebih besar dari bagian atasnya. (kiri kecil kanan besar).